第0章 リードソロモン符号とは
リードソロモン符号は誤り訂正符号の1つです。強力な誤り訂正能力を少ない計算量で実現でき、地上波ディジタル放送、衛星通信、CD、DVD、HDD、QRコードなど様々な分野で活用されています。 ここでは、リードソロモン符号の基礎について下記の各章で分かりやすく説明します。
第1章 ガロア体とガロア拡大体
リードソロモン符号を理解するためには、ガロア体およびガロア拡大体について知ることが不可欠である。リードソロモン符号はガロア体理論に基づいて構成される符号であり、その処理単位であるシンボルはガロア拡大体の元であるからである。
そもそも“体”とは特別な集合であり、集合内部で四則演算が閉じているなどの特徴を持っている。たとえば、実数全体や複素数全体などは体を構成する。これらの体は含まれる元の数が無限であるが、元の数が有限の体も存在し、これをガロア体(Galois Field)と呼ぶ。ガロア体は、整数を素数で除算した余りの集合により構成することができる。例えばガロア体GF(5)は、整数を5で除算した余りの集合であり、0,1,2,3,4の5つの元で構成される。GF(5)における加算と乗算は、表1-1および表1-2のように行うことができる。
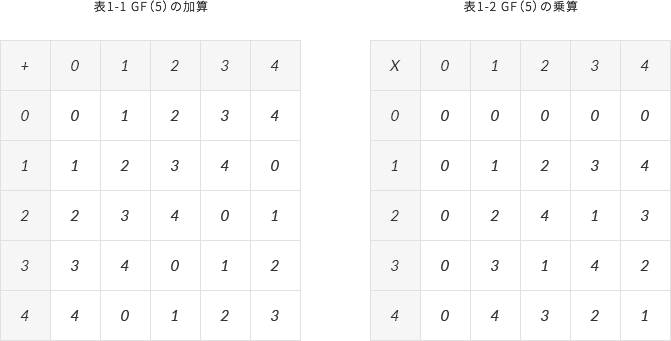
減算が行えるかどうかは、すべての元が加算に関する逆元を持っているかどうかを調べればよい。0,1,2,3,4の逆元は、それぞれ0,4,3,2,1であることから、 GF(5)は減算が可能であることが分かる。同様に、除算が行えるかどうかは、0以外の元が乗算に関する逆元を持っているかどうかを調べればよい。1,2,3,4の逆元は、それぞれ1,3,2,4であることから、GF(5)は除算が可能であることが分かる。 リードソロモン符号は、GF(2)をベースに構成することが多い。GF(2)の元は、0,1の2つであり、式1-1のように四則演算を行うことができる。
【式1-1】
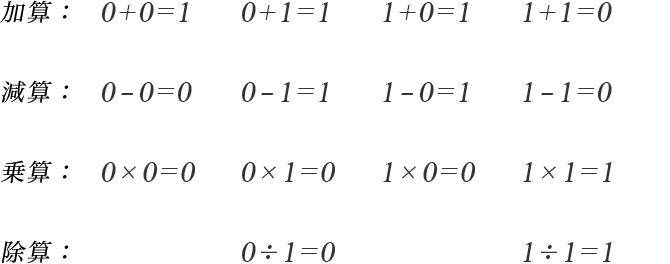
次に、GF(2)の元を係数とする多項式(GF(2)上の多項式と呼ぶ)を考える。GF(2)上の多項式をGF(2)上の既約多項式で除算した余りの集合が、ガロア拡大体である。 例えば、GF(2)上の4次の既約多項式(式1-2)で除算した余りの集合には、3次以下のGF(2)上の多項式16個がすべて含まれ、ガロア拡大体GF(2^4)を構成する。GF(2^4)の元を表1-3に示す。
【式1-2】

ガロア拡大体の元の表現には、多項式表現、べき表現、ベクトル表現の3種類がある。ガロア拡大体も体であるので、四則演算が可能である。加減算は多項式表現、乗除算はべき表現が便利である。
※補足1-1
ある元の逆元とは、演算すると単位元になる元のことである。例えば、加算に関する4の逆元を考える。表1-1から、4に1を加算すると0(単位元)になる。従って、4の加算に関する逆元は、1である。加算に関する逆元が存在すれば、その元による減算が可能になる。式1-3のように、逆元を用いて減算を加算に変えることができるからである。以上のことから、すべての元が加算に関する逆元を持っていれば、減算が行える。なお、乗算に関しても同様に考えることができる。但し、乗算に関する単位元は1であること、0の逆元は存在しない(0による除算はない)ことに注意が必要である。
【式1-3】

※補足1-2
GF(2)上の既約多項式とは、GF(2)上の多項式の積に因数分解できない多項式のことである。
※補足1-3
ガロア拡大体を構成するには既約多項式が必要である。しかしながら、リードソロモン符号で用いるガロア拡大体を構成するには既約なだけでは不十分であり、原始多項式を用いる必要がある。
第2章 リードソロモン符号の符号化・復号
リードソロモン符号の処理単位であるシンボルは、ガロア拡大体GF(2^m)の元である。一般によく用いられるリードソロモン符号のシンボルは8ビットであり、GF(2^8)の元である。 以下では簡単のため、表1-3に示すGF(2^4)上のリードソロモン符号を例として、符号化および復号を説明する。
2-1. 符号の設計
リードソロモン符号の設計とは、以下の2つのパラメータを決定することである。
- 1. 情報シンボル数(k):符号化を行う情報の単位(k×4ビット)
- 2. 訂正シンボル数(t):誤り訂正可能なシンボル数
訂正シンボル数がtの場合、必要となる冗長シンボル数は2tであり、kとtを決定すると符号シンボル数nは自動的に決まる(式2-1)。
【式2-1】

ここで、GF(2^4)上のリードソロモン符号のnの最大値は15であるため、nが15以下になるようにkとtを決定する必要がある。
2-2. 符号化
符号化には生成多項式が必要であり、式2-2に示す。
【式2-2】
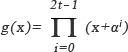
符号化は冗長シンボルを求める作業であり、情報多項式を生成多項式で割った余りとして求めることができる。
k=11、t=2の場合の符号化について、具体例を以下に示す。符号化する情報ビット系列をシンボルに変換し(図2-1)、情報多項式で表現する(式2-3)。

【式2-3】
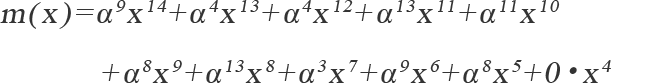
生成多項式は、式2-4で表わされる。
【式2-4】
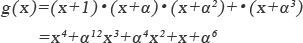
情報多項式を生成多項式で割った余りとして冗長多項式が求められる(式2-5)。
【式2-5】
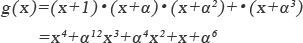
以上から、符号多項式は式2-6となり、図2-2のように符号化後のビット系列を得ることができる。
【式2-6】

2-3. 復号
復号手順を以下に示す(Step1~Step5)
- Step1:受信系列からシンドロームを求める。
- Step2:シンドロームを用いて、誤り位置多項式を求める。
- Step3:誤り位置多項式の根を求め、それが誤り位置を示す。
- Step4:誤り評価多項式を用いて、誤りの大きさを求める。
- Step5:求められた誤り位置と大きさを用いて訂正を行い、復号結果を得る。
なお、復号手順のうちStep2が最も多くの計算量を要する。Step2の手法としては、Peterson法、Berlekamp-Massey法、Euclid法が知られている。 Peterson法と比較して計算量の少ないBerlekamp-Massey法あるいはEuclid法が用いられることが多い。※補足2-1
リードソロモン符号の設計について、実際には情報シンボル数や訂正シンボル数の他にも、原始多項式や生成多項式の根の選択を行う必要がある。しかしながら、これらの選択は誤り訂正能力自体には影響を与えないため、ここでは触れない。
※補足2-2
GF(2^m)上のリードソロモン符号の符号シンボル数nの最大値は2^m -1である。
第3章 リードソロモン符号の訂正能力とその選定
リードソロモン符号の訂正能力tは、式3-1で表わされる。但し、nは符号シンボル数、kは情報シンボル数である。
【式3-1】
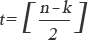
n-kは冗長シンボル数を表すことから、4シンボルの誤りを訂正するには8シンボルの冗長シンボル、8シンボルの誤りを訂正するには16シンボルの冗長シンボルを付加すればよいことが分かる。 このことから、リードソロモン符号の最小距離dminは式3-2で表すことができる。
【式3-2】
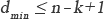
ここで、シングルトンの限界式(式3-3)を考える。
【式3-3】
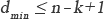
シングルトンの限界式は、最小距離が“冗長シンボル数+1”以下にしかならないことを意味している。式3-2と式3-3から、リードソロモン符号の最小距離はn-k+1となる。 従って、リードソロモン符号はシングルトンの限界式を等号で満たし、この意味においても非常に良好な符号であるといえる。
リードソロモン符号の誤り訂正はシンボル単位で行われることに注意が必要である。n=15、k=11、t=2のGF(2^4)上のリードソロモン符号について、 訂正可能な例と訂正不可能な例を図3-1に示す。図3-1から、訂正可否は誤りビット数で決まるのではなく、誤りシンボル数で決まることが分かる。

最後に、リードソロモン符号を実際のシステムに適用するときの、訂正能力の決定方法について考えてみる。システムには保障すべき誤り率があり、 それを達成するのに必要な訂正能力tをリードソロモン符号に持たせることになる。その値は、式3-4を用いた誤り率計算で求めることができる。Psは、通信路で発生するシンボル誤り率である。
【式3-4】
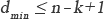
しかしながら、式3-4は、通信路で発生するシンボル誤りがランダムであることを仮定した式である。実際には完全にランダムであることは稀であり、2シンボル連続エラーや3シンボル連続エラーが頻繁に発生することもある。その場合、復号後の誤り率は大幅に劣化する。数万倍、数十万倍といったオーダーで劣化することも珍しくない。式3-4で計算した誤り率をベースに訂正能力を決定していた場合には、システムを稼働させた時点で愕然とすることになる。これを避けるためには、シンボルエラー分布の特徴をつかみ、それを考慮した計算式で誤り率を見積もる必要がある。
本技術解説を参考にし、必要なリードソロモンの選定が完了すれば、次はRTLの設計が必要となる。株式会社シグリードで提供しているリードソロモン符号生成ツールを用いると、リードソロモン符号の各種パラメータを指定するだけで、弊社IP(Si2520)をベースとしたRTLを自動生成する。また、消失(イレージャ)訂正、外部メモリ、エラー訂正シンボル数制限機能の有無なども指定可能である。
株式会社シグリードでは、リードソロモン符号だけでなく、他の既存の誤り訂正符号やシグリード オリジナルの誤り訂正符号も含めた複数の誤り訂正符号の中から、最も効果的な誤り訂正符号を提案するサービスも用意しており、受託設計サービスとの組み合わせにより、周辺回路も含んだトータルソリューションを提供することが可能である。
※補足3-1
最小距離についての説明は、“誤り訂正符号の技術解説”に記載している。
※補足3-2
シングルトンの限界式を等号で満たす符号を最大距離分離符号(Maximum Distance Separable Code; MDS符号)と呼ぶ。
す符号を最大距離分離符号(Maximum Distance Separable Code; MDS符号)と呼ぶ。