第0章 誤り訂正符号とは
誤り訂正符号とは一言で言ってしまうと、伝送路で発生する誤りを訂正する技術です。パソコンを使った有線/無線インターネット、携帯電話を使ったデータ通信、ワンセグ、HDDやBlu-Rayといったストレージなど、 様々な伝送路において誤り訂正符号は活躍しています。
ここでは、誤り訂正符号とは何なのかを下記の各章で分かりやすく説明します。
第1章 誤り訂正符号の原理
誤り訂正符号は、送信する情報に冗長を持たせることにより、伝送路で発生する誤りを訂正する技術である。具体的な符号化、復号の例を図1-1に示す。
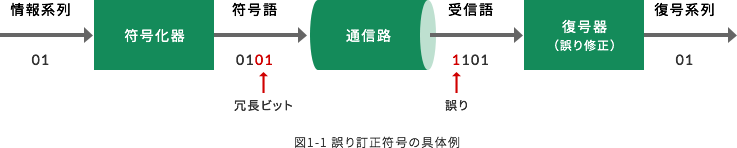
符号化器は、情報系列に冗長ビットを付加する。通信路で発生したビット誤りを訂正するのが復号器である。復号器は、付加されている冗長ビットを用いて誤りを訂正する。 誤りを訂正できる原理は極めて数学的であり、その理論を深く理解するには多くの時間を必要とするが、視覚的に分かりやすく説明する図を図1-2に示す。なお、図1-2では具体例として、2ビットの情報に2ビットの冗長を付加する誤り訂正符号を用いている。
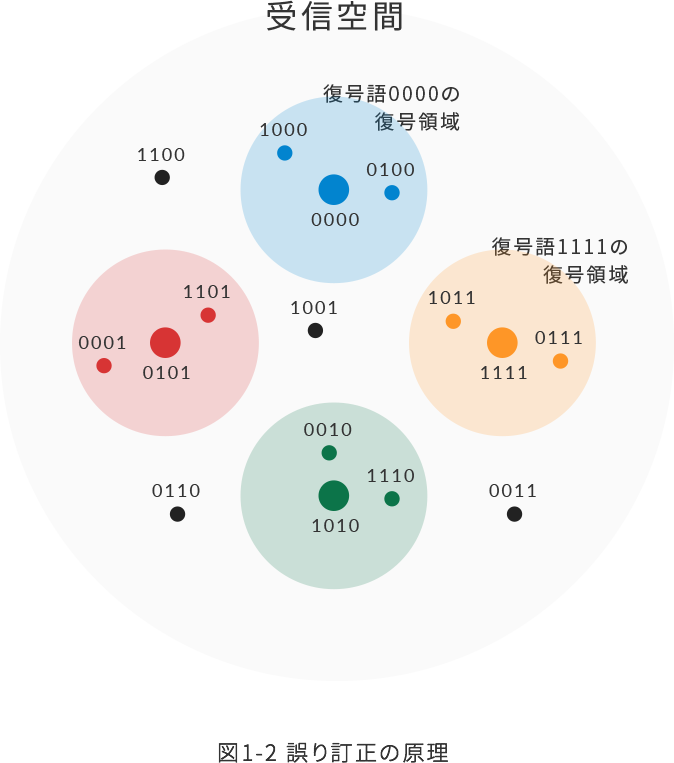
図1-2は受信空間を表しており、今回の例では4ビットのベクトル空間となる。このベクトル空間には16個の点が存在し、このうち4個の点(0000, 0101, 1010, 1111)が正しい符号語に対応する。これらの点を受信すると、復号器は、誤りが発生していないと判断する。その他の12個の点を受信したときに復号器で行われる処理は、次の2つのケースに分けられる。
| ケース 1 | 各符号語の復号領域内の点を受信したとき → 1ビットの誤りを訂正し、各符号語を復元する |
|---|---|
| ケース 2 | 復号領域外の点を受信したとき → 訂正できない誤りが発生したと判断する |
以上のことから、復号系列を受け取るシステムの立場から見た場合、誤り訂正の成否は表1-1に示す3通りに分類できる。 なお、“訂正可能”と“誤訂正”は復号器では区別できないため、区別が必要な場合は別途誤り検出符号(CRCなど)を導入する必要がある。
表1-1 誤り訂正の結果
| 誤り訂正の成否 | 説明 |
|---|---|
| 訂正可能 | 受信語が、送信した符号語の復号領域に入った場合 |
| 誤訂正 | 受信語が、送信した符号語と異なる符号語の復号領域に入った場合 |
| 訂正不可能 (誤り検出) | 受信語が、どの符号語の復号領域にも入らなかった場合 |
※補足1-1
説明のために用いた誤り訂正符号は、情報系列に冗長ビットを付加する。このように、符号語に情報系列がそのままの形で表れる符号を組織符号と呼ぶ。誤り訂正符号としては組織符号が用いられることが多いが、組織符号でない誤り訂正符号も存在する。※補足1-2
説明のために用いた誤り訂正符号は、正確には1ビット誤り訂正符号ではない。全ての1ビット誤りを訂正できないからである。例えば、符号語0000を送信したときに1ビット誤りが発生した場合を考えると、1000や0100を受信したときは訂正可能であるが、0010や0001を受信したときは誤訂正となる。※補足1-3
説明のために用いた誤り訂正符号はビット単位で処理を行う符号であるが、リードソロモン符号のようにシンボル単位で処理を行う誤り訂正符号もある。リードソロモン符号は、任意のビット数を1シンボルと考えて符号を構成することができる。
第2章 誤り訂正符号の訂正能力
誤り訂正符号の訂正能力は、ハミング距離を用いて考えることができる。2つのシンボル間のハミング距離dhの定義を式2-1に示す。すなわち、同じシンボル間のハミング距離は0、異なるシンボル間のハミング距離は1である。
【式2-1】
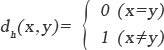
また、2つのn次元ベクトル間のハミング距離dhの定義を式2-2に示す。式2-2より、2つのベクトル間のハミング距離は、異なるシンボルの数に等しい。
【式2-2】
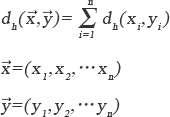
ハミング距離の具体例として、4つのベクトル(0000,0101,1010,1111)を符号語として持つ符号について、任意の異なる2つの符号語のハミング距離を表2-1に示す。
表2-1 ハミング距離の具体例
| 符号語1 | 符号語2 | ハミング距離 |
|---|---|---|
| 0000 | 0101 | 2 |
| 0000 | 1010 | 2 |
| 0000 | 1111 | 4 |
| 0101 | 0000 | 2 |
| 0101 | 1010 | 4 |
| 0101 | 1111 | 2 |
| 符号語1 | 符号語2 | ハミング距離 |
|---|---|---|
| 1010 | 0000 | 2 |
| 1010 | 0101 | 4 |
| 1010 | 1111 | 2 |
| 1111 | 0000 | 4 |
| 1111 | 0101 | 2 |
| 1111 | 1010 | 2 |
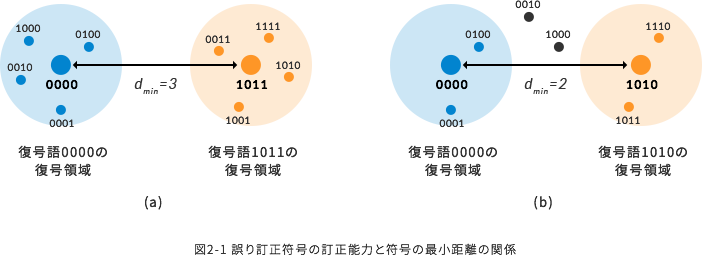
表2-1より、この符号の任意の異なる2つの符号語の距離の最小値は、2であることが分かる。これを符号の最小距離dminと呼ぶ。 誤り訂正符号の訂正能力は、最小距離を用いて表すことができる。符号がt個以下の誤りを全て訂正するための必要十分条件を式2-3に示す。
【式2-3】
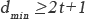
式2-3より、1個の誤りを訂正するためには、最小距離が3以上でなければならない。これは、図2-1のように考えると分かりやすい。(a)は最小距離が3の場合の図であり、各符号語から距離1のベクトル全てを復号領域に含めることができる。 従って、1個の誤りを全て訂正することができる。(b)は最小距離が2の場合の図であり、各符号語から距離1のベクトル全てを復号領域に含めることができない。なぜなら、ベクトル0010と1000は、符号語0000と1010の両方からの距離が1となるからである。従って、1個の誤り全てを訂正することができない。
※補足2-1
1シンボルが1ビットの場合についてハミング距離や訂正能力について説明したが、1シンボルが複数ビットの場合についても同様である。※補足2-2
誤り“検出”能力も最小距離を用いて表すことができる。符号がt個以下の誤りを全て検出するための必要十分条件を式2-4に示す。
【式2-4】

第3章 誤り訂正符号の選定
誤り訂正符号には、ハミング符号やリードソロモン符号など、様々な種類の符号が存在する。小さい回路規模で実装可能な符号、理論限界に近い訂正能力を有する符号など、符号によってその特徴は異なる。従って、発生する誤りの特徴やアプリケーションの要求に応じて、最適な誤り訂正符号を選択する必要がある。
また、リードソロモン符号を用いると決定した場合でも、どの程度の訂正能力を持たせるのが最適であるかを検討する必要がある。例えば表3-1のような通信に、1シンボルが8ビットのリードソロモン符号を適用することを考える。

誤り訂正符号を用いない場合のブロック誤り率Pbは、NとPsを用いて式3-1のように計算できる。保証したいブロック誤り率Pとは大きく乖離していることが分かる。
【式3-1】
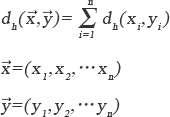
この通信に、1ブロックあたりの誤り訂正能力がTシンボルのリードソロモン符号を適用した場合、誤り訂正後のブロック誤り率Pcは式3-2で計算できる。式中のCは、組み合わせを表す。訂正シンボル数Tとブロック誤り率Pcの関係を式3-2で求めた結果を図3-1に示す。図3-1より、保証したいブロック誤り率Pを達成するためには、訂正シンボル数Tが5のリードソロモン符号を用いればよいことが分かる。
【式3-2】
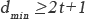
しかしながら、上記の訂正シンボル数決定方法には大きな問題点がある。リードソロモン符号によって付加される冗長シンボルの分だけ、送信できる情報が減少することを考慮していないためである。アプリケーションにとって、保証したいブロック誤り率を達成することは重要であるが、情報の送信レートの目標値達成も同様に重要である。 情報の送信レートを保ちながらリードソロモン符号を適用するには、どうすればよいのだろうか?一つの解決策は、通信速度を上げることである。上記のT=5のリードソロモンの場合、付加される冗長シンボル数は10である。従って、通信速度を128/118倍にすることで情報の送信レートを保つことができる。 なお、通信速度を上げると、通信路で発生するシンボル誤り率Psが悪化することが普通である。これを考慮すると、訂正シンボル数Tとブロック誤り率Pcの関係は図3-2に示すような曲線を描く。保証したいブロック誤り率を達成可能な最小の訂正シンボル数を選択することにより、最小の回路規模で所望の性能を得ることができる。

全てのシステムには、それぞれ最適な誤り訂正符号とその訂正能力というものが存在する。その最適解を見つけるには、情報の送信レート、電力、LSIのコスト、情報の送信環境(ノイズ環境など)といったことを総合的に検討する必要があり、本当に最適解を選択できているのか不安になることが多い。
株式会社シグリードでは、その最適解を提案するサービスを提供している。既存の誤り訂正符号だけでなく、シグリード オリジナルの誤り訂正符号を提案することも可能である。また、受託設計サービスとの併用により、高速・低電力・省面積の回路として提案することができるだけでなく、誤り訂正符号の周辺回路も含んだトータルソリューションを提供することが可能である。
※補足3-1
シンボル誤り率は、“誤ったシンボル数/送信した全シンボル数”で計算することができる。
ブロック誤り率は、“誤ったブロック数/送信した全ブロック数”で計算することができる。
※補足3-2
式3-2でリードソロモン符号による誤り訂正後のブロック誤り率を計算することができるが、通信路で発生するシンボル誤りが完全にランダムであることを前提にした式である。実際の通信路では、シンボル誤りがバースト状に発生することが多く、ブロック誤り率は式3-2で求めた結果と大きく乖離するケースがほとんどである。ブロック誤り率を正しく計算するには、通信路で発生するシンボル誤りのバースト特性を観測し、より複雑な数式で誤り率を計算する必要がある。
シグリードでは、特定のシステムに最適な誤り訂正符号を検証・選定するサービスも行っております。既存の誤り訂正符号だけでなく、シグリード オリジナルの誤り訂正符号も含めた複数の誤り訂正符号の中から、最も効果的な誤り訂正符号をご提案します。受託設計サービスとの組み合わせにより、周辺回路も含んだトータルソリューションをご提供することも可能です。詳しくは弊社担当者までご連絡ください。